Ieee 754
from bleistift2@sopuli.xyz to science_memes@mander.xyz on 02 Jan 22:05
https://sopuli.xyz/post/20980837
from bleistift2@sopuli.xyz to science_memes@mander.xyz on 02 Jan 22:05
https://sopuli.xyz/post/20980837
cross-posted from: lemmy.ml/post/24332731
StolenCross-posted from here: fosstodon.org/@foo/113731569632505985
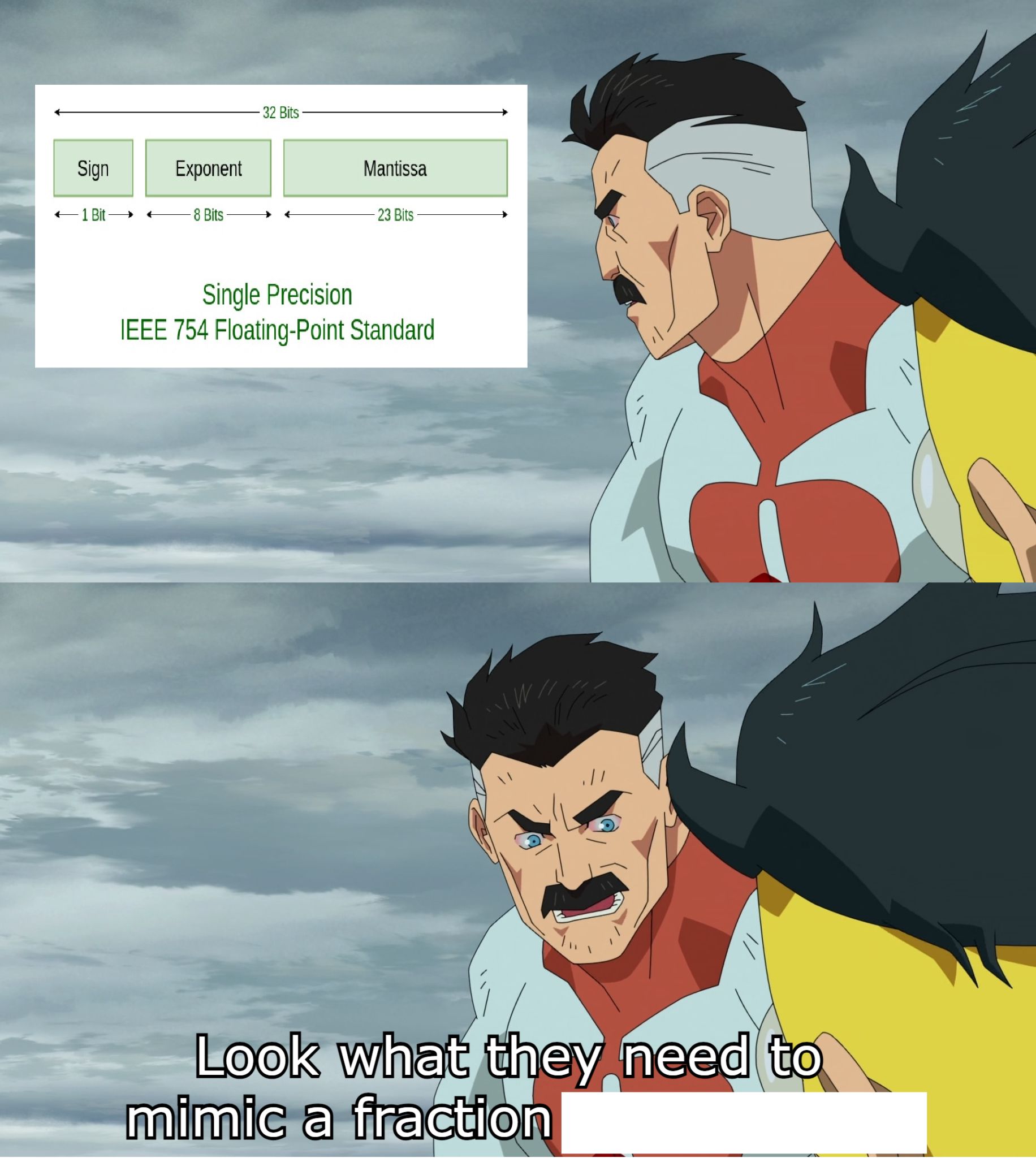
threaded - newest
negative zero is real
Well, duh. All fractions are real.
except for the imaginary ones
Until you construct a square with them.
ℚ ⊂ ℝ ⊂ ℂ, at least that’s how I was taught.
LOL! Man I learned that in college and never used it ever again. I never came across any scenarios in my professional career as a software engineer where knowing this was useful at all outside of our labs/homework.
Anyone got any example where this knowledge became useful?
If you’re doing any work with accounting, or writing test cases with floating point values.
Please tell me you aren’t using floating points with money
Knowing not to use floating point with money is good use of that knowledge.
You’d be dismayed to find out how often I’ve seen people do that.
Yeah I shudder when I see floats and currency.
That sounds like an explosive duo
Eh, if you use doubles and you add 0.000314 (just over 0.03 cents) to ten billion dollars you have an error of 1/10000 of a cent, and thats a deliberately perverse transaction. Its not ideal but its not the waiting disaster that using single precision is.
How do you do money? Especially with stuff like some prices having three or four decimals
Instead of representing $1.102 as
1.102your store it as1012(or whatever precision you need) and divide by 1000 only for displaying it.So if you handle different precisions you also need to store the precision/exponent explicitly for every value. Or would you sanitise this at input and throw an exception if someone wants more precision than the program is made for?
It depends on the requirements of your app and what programming language you use. Sometimes you can get away with using a fixed precision that you can assume everywhere, but most common programming languages will have some implementation of a decimal type with variable precision if needed, so you won’t need to implement it on your own outside of university exercises.
Okay thank you. I was wondering because for stuff like buying electricity, gas or certain resources, parts etc. there is prices with higher precision in cents, but the precision would not be identical over all use cases in a large company.
No exponent, or at least a common fixed exponent. The technique is called “fixed point” as opposed to “floating point”. The rationale is always to have a known level of precision.
No. I don’t have to remember that.
I just have to remember the limits and how you can break the system. You don’t have to think about the representation.
It’s useful to know that floats don’t have unlimited precision, and why adding a very large number with a very small number isn’t going to work well.
And this is why f64 exists!
Yeah but you don’t really have to think about how it works in the background ever time you deal with that. You just know.
You learn how once and then you just remember not to do that and that’s it.
I agree we don’t generally need think about the technical details. It’s just good to be aware of the exponent and mantissa parts to better understand where the inaccuracies of floating point numbers come from.
How long has this career been? What languages? And in what industries? Knowing how floats are represented at the bit level is important for all sorts of things including serialization and math (that isn’t accounting).
More than a surface level understanding is not necessary. The level of detail in the meme is sufficient for 99,9% of jobs.
No, that’s not all just accounting, it’s pretty much everyone who isn’t working on very low level libraries.
What in turn is important for all sorts of things is knowing how irrelevant most things are for most cases. Bit level is not important, if you’re operating 20 layers above it, just as business logic details are not important if you’re optimizing a general math library.
Since 2008.
I’ve worked as a build engineer, application developer, web developer, product support, DevOps, etc.
I only ever had to worry about the limits, but never how it works in the background.
Writing floating point emulation code?
I’d pretty much avoided learning about floating point until we decided to refactor the softfloat code in QEMU to support additional formats.
The very wide majority of IT professionals don’t work on emulation or even system kernels. Most of us are doing simple applications, or working on supporting these applications, or their deployment and maintenance.
h14s.p5r.org/2012/09/0x5f3759df.html comes to mind
To not be surprised when
0.1 + 0.1 != 0.2In game dev it’s pretty common. Lots of stuff is built on floating point and balancing quality and performance, so we can’t just switch to double when things start getting janky as we can’t afford the cost, so instead we actually have to think and work out the limits of 32 bit floats.
So you have to remember how it’s represented in the system with how the bits are used? Or you just have to remember some general rules that “if you do that, it’ll fuck up.”
Well, rules like “all integers can be represented up to 2^24” and “10^-38 is where denormalisation happens” are helpful, but I often have to figure out why I got a dodgy value from first principles, floating point is too complicated to solve every problem with 3 general rules.
I wrote a float from string function once which obviously requires the details (intentionally low quality and limited but faster variant since the standard version was way too slow).
Accumulation of floating point precision errors is so common, we have an entire page about why unit tests need to account for it.
It’s not mimicry.
finally a clever user of the meme